Arithmetic sequences

A sequence is an ordered list of numbers. The numbers in a sequence are called elements (or terms) of the sequence. A series is the sum of a sequence. The resulting value is called the sum (or summation). For example, if a sequence has elements , then is the corresponding series, and the sum is In this section, we will focus on arithmetic sequences and geometric sequences.

An arithmetic sequence is a sequence of numbers with the same difference between consecutive terms. That constant difference, , is called the common difference. For example, the sequence is an arithmetic sequence that starts with 1 and ends with 100. The common difference is 1. All the multiples of 5 between 1 and 200 () is also an arithmetic sequence. The sequence starts with 5, ends with 200, and has a common difference of 5. If the first term of an arithmetic sequence is and the common difference is , the n-th term in the sequence is

How many numbers are in the sequence of ? Clearly, it is 100.

How many numbers are in the sequence of ? If we subtract 50 from each element in the sequence, we get the sequence of . The sequence of has 100 elements as well.

How many numbers are in the sequence of ? It is . If we subtract from all elements in the series, the series becomes . Therefore, the sequence has elements.

How do we calculate the sum of an arithmetic sequence? The legendary mathematician Gauss offered an approach in the late 1700s. When he was a pupil in elementary school, his teacher gave the children a boring assignment to add the numbers from 1 to 100. To the amazement of the teacher, Gauss turned in his answer in less than a minute. The following was his approach:

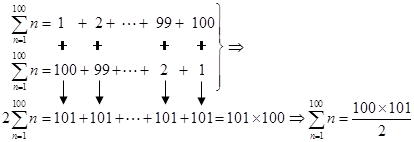
Essentially, he noticed that the first number and the last number add up to 101; the second number and the second to last number add up to 101; the third number and the third to last number also add up to 101… Therefore, the average of the numbers in the sequence is . Since there are 100 numbers in the sequence, the sum is For any integer N, the sum of is .

Let’s further expand the equation to any series that starts with M and ends with N. The average of the numbers in the series is . Since the sequence has elements, the sum of the sequence is:

In general, the sum of an arithmetic sequence that starts with M, ends with N, and has a common difference of k is

The first term on the right-hand side of the equation is the average of the numbers in the arithmetic sequence. It again equals the average of the sequence’s first element and the sequence’s last element. The second term on the right-hand side of the equation is the number of elements in the arithmetic sequence.

In the case of the series of all the multiples of 5 between 1 and 200, the common difference is 5, and the sum of the sequence is

Using the general equation, we can also get the sum of the first odd numbers:

Which of the following sequences has the largest average?

(A)  multiples of 3 between 1 and 200

(B)   multiples of 4 between 1 and 200

(C)   multiples of 5 between 1 and 200

(D)  multiples of 6 between 1 and 200

Solution: Since the average of numbers in the arithmetic sequence is the average of the sequence’s first number and the sequence’s last number, we only need to evaluate the sum of the first number and the last number in each sequence. The (first number, last number) is (3, 198) in A, (4, 200) in B, (5, 200) in C, and (6, 198) in D. Since C has the largest sum of the first number and the last number, it has the largest average.

A clock (numbered 1 – 12 clockwise) fell off the wall and broke into three pieces. You find that the sums of the numbers on each piece are equal. What are the numbers on each piece? (No strange-shaped piece is allowed.)

Solution: Using the summation equation, we have . Thus, the numbers on each piece must sum up to 26. On the step to identify the numbers on each piece, one may get stuck if one assumes that the numbers on each piece have to be consecutive (because no strange-shaped piece is allowed). It’s easy to see that 5, 6, 7, and 8 add up to 26. Then one cannot find more consecutive numbers that add up to 26. Such an assumption is not correct since 12 and 1 are neighbors on a clock. Once that wrong assumption is dropped, it becomes clear that and . Therefore, the second piece is 11, 12, 1, and 2; the third piece is 3, 4, 9, and 10.

What is the value of

Solution: One approach is to separate the positive and negative terms and apply the summation formula:

Another approach is to group consecutive odd and even number terms:

How many 1s are in sequence? It is equal to the number of elements in the sequence of . Therefore, the value is .

A number is taken out of the arithmetic sequence . If the sum of the remaining numbers in the sequence is what is the value of

Solution: Since and is between 1 and , the sum of the remaining numbers is between and Because is close to is close to 80.

Let’s start with . If then If then . We can take out to make the remaining numbers add up to . If even if we take out the largest number 81, the remaining numbers add up to . Therefore, and we have

is an arithmetic sequence with a common difference of 2. If the sum of is 100, what is

Solution: Since the common difference is 2, we have and

Therefore,

Numbers are placed in the circles of Figure 2‑1 so that the numbers on all three edges of the triangle add up to the same number, . What is the largest possible value of

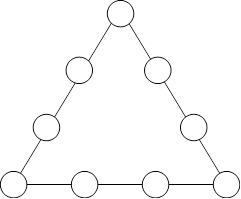
Figure 2‑1 Triangle of numbers

Solution: The numbers at the three vertices of the triangle are shared by two edges; they are used twice in the summation of the edges. The remaining six numbers are used once. To make the sum of the edges as large as possible, we should assign the largest values in the sequence to the vertices, which are . When we add all three edges up, we get

But can we assign to the reaming six circles to make all edges have the same sum? As shown in the following table, in order to do so, we need to split 1-6 to three pairs that add up to and respectively. The last column shows the pairs. Therefore, the largest possible value of is indeed 23.

If are integers that satisfy and what is the maximum value of ?

Solution: To make as large as possible, we want to make as large as possible. Let’s start with getting the max value of

We have and the max value of is

If and we have

The maximum value of is

If and we have

Therefore, the max value of

You may question the solution as we conditioned on maximum value to get maximum value and then conditioned on max value to get maximum value. If there is no gap between them (i.e., and , there is no question that is maximized. Since is it possible to get a larger sum by shuffling

It is true that does not need to be its max value to make the maximum value. For example, give us the same sum. Can we make the sum larger than Not if When and What if we make instead? We get Therefore, we confirm that is indeed the maximum.

Counterfeit coins: There are 10 bags with 100 identical coins in each bag. In all bags but one, each coin weighs 10 grams. However, all the coins in the counterfeit bag weigh either 9 or 11 grams. Can you find the counterfeit bag in only one weighing, using a digital scale (that tells the exact weight)? [9]

Solution: Yes, we can identify the counterfeit bag using one measurement. Take 1 coin out of the first bag, 2 out of the second bag, 3 out the third bag..., and 10 coins out of the tenth bag. Altogether, there are coins. If there were no counterfeit coins, they should weigh 550 grams. Let’s assume the i-th bag is the counterfeit bag. There will be counterfeit coins and the final weight will be Since i is distinct for each bag, we can identify the counterfeit coin bag as well as whether the counterfeit coins are lighter or heavier than the real coins using This is not the only answer: we can choose other numbers of coins from each bag as long as they are all different numbers.