. Why is that the case?
The reason lies in the Binomial Theorem:One observation of Pascal’s Triangle is that all the numbers
on the n-th row add up to . Why is that the case?
The reason lies in the Binomial Theorem:
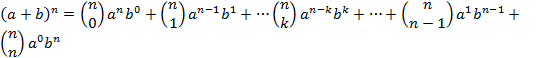
From basic algebra, we know that:
Although we can prove the Binomial Theorem using induction,
let’s focus on the intuition behind it instead. The Binomial Theorem
essentially states that the coefficient of 
is 
. Let’s expand 
and think about why the
Binomial Theorem holds:
Each term in involves choosing 
or 
from
each of 
different binary choices
(between and ). The
term means that 
and 
are chosen from choices.
Since there are ways, the coefficient of
is .
The Binomial Theorem shows why all the numbers on the n-th
row add up to . The elements on the n-th
row are 
. If 
and 
, the
expansion of becomes:
Problem 3‑29
Expand 
.
Solution:
If we apply the binomial theorem to 
we get the following
expanded terms:
Problem 3‑30
«« 100th digit: What is the 100th digit to the right of
the decimal point in the decimal representation of 
? (Hint: 
. What will happen to 
as n becomes large?)
Solution: If you
still have not figured out the answer from the hint, here is one more hint: 
is an integer when 
.
Applying the binomial theorem for 
, we have
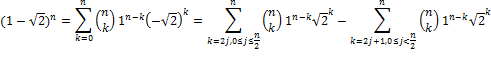
So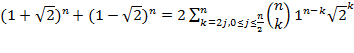 
, which is always an
integer. It is easy to see that 
. Therefore, the 100th
digit of 
must be 9.
Problem 3‑31
Part A. Cube of an integer: Let x be an integer between 1 and 1012. What is the probability that the cube of x ends with 11?[13]
Part B. What is the tens digit of 
?
Solution:
All integers can be expressed as 
, where is the
last digit of x. Applying the binomial theorem, we have 
.
The unit digit of 
only depends on 
So 
has a unit digit of 1.
Only satisfies this
requirement and 
. Since , the tenth digit solely
depends on 
. Therefore, 
must
end in 1, which requires the last digit of b to be 7. Consequently, the
last two digits of x should be 71, which has a probability of 1% for
integers between 1 and 1012.
For part B, since the last 2 digits of 
only depends on the last
two digits of 
the tens digit of is the same as the tens
digit of 
Let’s again apply the
binomial theorem:
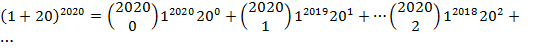
Since all the terms except for 
in
the equation are multiples of 
the tens digit is the
same as the tens digit of 
Thus, the tens digit of
is 0.
General Rule: The binomial theorem is a useful tool to determine the unit and tens digit of exponentials.
Problem 3‑32
is a 2-digit integer. If
the last two digits of are 57, what is 
Solution:
Let’s start with the units digit. The units digit of only depends on the
units digit of . We have:
.
The units digit must be 3. Now let’s write 
and
express as 
The tens digit of 
only depends on 
. For
the tens digit of to be 5, the units
digit of 
must be 3. Among
integers 1-9, 
Therefore, 
[13] Hint: The last two digits
of 
only depend on the last
two digits of x.