Combinations

With permutations, the order of the selected items matters. If the order of items selected into a subset does not matter, we have combinations. The number of combinations of distinct items taken at a time (order doesn’t matter) is:

is called “ choose ”.

Note that the number of combinations is an application of an overcounting correction: We are arranging objects, of which objects are alike and the rest objects are alike.

is to choosing items into a group from items. It is equivalent to choosing items into another group from items. Therefore, . We can easily prove the identity using the formula as well:

One inference from the number of combinations is that the product of any consecutive integers is divisible by

Powerball: What is the probability of winning Powerball if you buy a Powerball ticket? Powerball is a multi-state lottery[11] offered in most of the United States. The game sequentially randomly draws 5 balls from 69 balls labeled from 1 to 69 without replacement and then draws a separate Powerball from 26 balls labeled from 1 to 26. A lottery buyer chooses five numbers from 1 to 69 and then selects a Powerball number from 1 to 26. If both the set of five numbers (orders do not matter) and the Power number match the drawings, the ticket wins the Powerball.

Solution: The number of possible outcomes of drawing 5 balls from 69 balls labeled from 1 to 69 is a combination. The number of combinations can be calculated as

The number of possible outcomes of drawing the Powerball is 26. Since these two steps are independent, the total number of possible outcomes is

Therefore, the probability of winning the Powerball is 1/292201338.

In how many ways can the letters in the word BANANA be arranged?

Solution: This is the same as Problem 3‑12. Let’s solve the same problem using combinations. The word BANANA has 6 letters: 3 As, 2Ns, and 1 B. We need to put these letters into 6 “seats.” First, we choose the seats for A. We need to choose 3 seats from 6 seats. Since As are indistinguishable, the orders do not matter. Therefore, the number of combinations is Among the remaining 3 seats, we need to choose 2 for Ns. The number of combinations is Applying the basic principle of counting, the total number of ways is

The combination approach shows that the link between permutation and combination is the principle of overcounting. Because the order of the k selected items does not matter in a combination, it is equivalent to that the items are indistinguishable. Therefore, we correct the overcounting by dividing the number from permutation by

How many ways can you put 3 white rooks (assuming they are indistinguishable) on an chessboard so that no two rooks share the same row or column?

Solution: We can put the first rook in any of the 64 squares, which eliminates one row and one column from the board as the rest of the rooks cannot be in the same row or column. After eliminating one row and one column, the chessboard becomes a one. Thus, the second rook has 49 choices. The second rook eliminates another row and another column and leaves a chessboard. Therefore, the total permutation is Since the rooks are indistinguishable, we need to divide the number by The total number of ways is

Part A. How many ways are there to distribute 10 apples to 4 children? Assume that each child may get to 10 apples.

Part B. If we assume that each child needs to get at least 1 apple, how many ways are there to distribute 10 apples to 4 children?

Solution: As shown in Figure 3‑4, if we put the 10 apples in a row on a table, distributing the apples to 4 children is equivalent to putting 3 dividers to separate the apples to 4 piles. Since a pile may have 0 apples, it means a divider may be to the left or right of all apples, and two dividers may be between the same two apples. The example in Figure 3‑4 divides the apples to piles of apples. We have 13 positions. 10 of the positions are allocated to the apples and the remaining 3 to dividers. It is equivalent to choosing a subset of 3 objects out of a total of 13 objects. Therefore, the number of ways to distribute 10 apples to 4 children is .

Figure 3‑4 Distributing items among groups

In part B, since each child needs to get at least 1 apple, we can first distribute 1 apple to each child. Then the problem becomes how many ways there are to distribute 6 apples to 4 children, assuming that each child may get 0 apples. Following part A’s logic, we get the solution .

Let’s consider another approach to solve part B that offers a different perspective. We still need 3 dividers to divide 10 apples. Since each pile cannot have 0 apple, we cannot put a divider to the left or the right of all apples. We cannot have two dividers between the same two apples either, as that will create a pile with 0 apples. As shown in Figure 3‑5, we need to choose dividers among the spaces that separate the 10 apples.

Therefore, the solution is .

Figure 3‑5 Distributing items among non-empty groups

General Rule: If we need to count the number of ways to distribute items among groups and each group may get 0 objects, the problem is equivalent to choosing dividers among places for dividers and objects. Therefore, the solution is .

If we need to count the number of ways to distribute items among groups and each group must have at least 1 object, the problem is equivalent to choosing dividers among possible places. Therefore, the solution is

Part A. and are nonnegative integers that satisfy In how many ways can we create such groups of and ?

Part B. Sophie is putting together a Halloween treat bag that contains 10 pieces of Hershey’s nuggets from three types of nuggets: milk chocolate, milk chocolate with almonds, and dark chocolate. How many different combinations are possible?

Solution: Both parts of this problem are equivalent to distributing 10 items among three groups (and ), and each group may get 0 objects. Therefore, there are 66 ways.

General Rule: When we encounter problems that allow the number of items in each group to vary, think about recognizing or converting the problem to a problem of distributing items among groups.

We will see another problem equivalent to distributing items among groups when we calculate the number of terms in multivariate polynomials.

If we assume that each child gets no more than 5 apples, how many ways are there to distribute 10 apples to 4 children?

Solution: The problem is easier to solve if we use complementary counting. Without restriction, the total number of choices is . Let’s consider the cases that one child does get more than 5 apples. In such cases, we first set aside 6 apples and give them to one of the kids. Since there are 4 apples left, that selected kid is the only one who has more than 5 apples and there are 4 choices of which kid to get the 6 apples set aside. Then we distribute the remaining apples to 4 children. The number of choices of the second step is . The number of choices where at least one child gets more than 5 apples is Therefore, the number of ways to distribute 10 apples to 4 children without anyone getting more than 5 apples is .

The Greenwich High School basketball team has 10 team members. The team needs to select five members to play in a basketball game. John and James are brothers who always play together. In other words, if one of the brothers is selected to play the game, the other brother must also be selected. How many possible ways are there to select a team?

Solution: Since special rules apply to John and James, let’s use the casework approach by considering different scenarios involving the selection of John and James. For each scenario, we estimate the possible ways to select a team. Because John and James can only be selected together, there are two possible cases:

Case 1. Both John and James are selected, in which case we select 3 members from the other 8 team members. There are possible combinations.

Case 2. Neither John nor James is selected, in which case we select 5 members from the other 8 team members. There are possible combinations.

Therefore, the total number of ways is

The Greenwich High School basketball team has 10 team members. The team needs to select five members to play in a basketball game. John and James are brothers. Since their parents are on a business trip, at least one of them needs to stay at home to babysit their kid sister. In other words, if one of the brothers is selected to play the game, the other cannot be selected. How many possible ways are there to select a team?

Solution: Since special rules apply to John and James, let’s again consider different scenarios involving the selection of John and James. For each scenario, we estimate the possible ways to select a team. Because John and James cannot be selected together, there are three possible scenarios:

Scenario 1. John is selected and James is not, in which case we need to select 4 members from the other 8 members. There are possible combinations.

Scenario 2. James is selected and John is not. There are possible combinations as well.

Scenario 3. Neither John nor James is selected. There are possible combinations.

Therefore, the total number of ways is

A different approach to solve the problem is to use complementary counting. If there is no restriction, the number of ways to choose a team is . Since John and James cannot be both selected for the team, we only need to exclude the cases that they are both selected. As discussed in the previous problem, there are possible combinations that they are both selected. Therefore, the number of ways is.

Complementary counting can be applied to the previous problem as well. We again start with 252 combinations if there is no restriction. Since John and James can only be selected together, we need to exclude two scenarios: John is selected and James is not; James is selected and John is not. In this problem, we have shown that either case has possible combinations. Therefore, the solution for the previous problem is

How many rectangles are in Figure 3‑6? A rectangle may be of different sizes ranges from to in the figure.

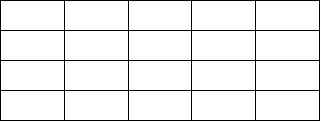
Figure 3‑6 Question: Number of rectangles

Solution: If we think in terms of the smallest rectangles as the building block, there are smallest rectangles. One way to solve the problem is to use casework by considering different sizes of the rectangle that we select. Let be the height and be the width We can build a table to track the number of rectangles of different sizes:

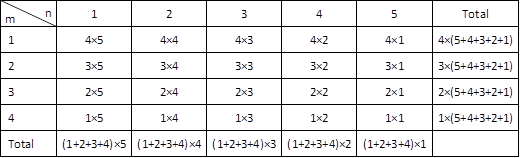
What’s the grand total? We can sum the totals by row or by column. Both give us the same result, Following this analysis, we also see a general rule for the total number of rectangles: If the largest rectangle includes small rectangles, the number of rectangles of all sizes are

Now let’s consider a different and more intuitive approach (once we understand the logic behind it). Rectangles are formed by the intersection of two horizontal lines and two vertical lines. A pair of horizontal lines and a pair of vertical lines identify a unique rectangle. As shown in Figure 3‑7, the number of horizontal lines to choose is (more generally ), and the number of vertical lines to choose is (more generally ). For example, choosing horizontal lines and vertical lines form the shaded rectangle. To form a rectangle, we choose any of two (unordered) horizontal lines and two vertical lines independently. The number of choices for two horizontal lines is and the number of choices for two vertical lines is . Therefore, the total number of rectangles is .

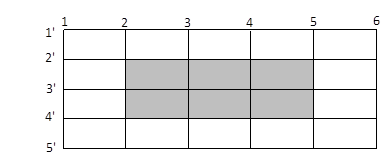
Figure 3‑7 Solution: Number of rectangles

General Rule: If the rectangle includes small rectangles, the number of rectangles of all sizes are =

As shown in Figure 3‑8, a grid is made of 25 small squares. How many squares are in Figure 3‑8? A square may be of different sizes ranges from to in the figure.

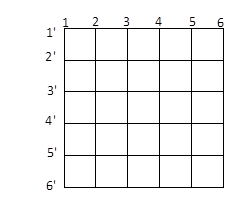
Figure 3‑8 Number of squares in a grid

Solution: Let’s start with square(s) of size There is only one choice: horizontal lines and are selected, and vertical lines and are selected. For squares of size there are 2 choices for horizontal line groups and 2 choices for vertical line groups The total number of combinations is Similarly, for squares of size there are combinations. For squares of size there are combinations. For squares with of size there are combinations. Therefore, the total number of squares is

General Rule: For a square grid, the total number of squares of different sizes is

How many possible ways are there to select three numbers from integers (orders do not matter) so that their product is an even number?

Solution: If there is no restriction, there are combinations. For their product to be an even number, there are three scenarios: 1 out of 3 is even; 2 out of 3 are even; 3 out of 3 are even. Instead of calculating each scenario and adding them up, we can exclude the ways to make the product to be an odd number from . The product of three numbers is odd if and only if all three numbers are odd, which means that we need to choose all three numbers from 50 odd numbers between 1 and 100 (). The number of combinations to choose three numbers from 50 odd number is . Therefore, the number of ways to select three numbers so that their product is an even number is .

Jason’s home (point A in Figure 3‑9) is 6 blocks west and 3 blocks south of the school (point B). Every day he walks along the bocks to get to school. If his route is as short as possible, how many different routes can he take?

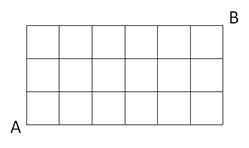
Figure 3‑9 Number of paths to school

Solution: The shortest route always includes 9 blocks: 3 blocks north and 6 blocks east. Therefore, the number of routes is simply choosing 3 blocks to go north out of 9 blocks:

Stephen’s home (point A in Figure 3‑10) is 7 blocks west and 7 blocks south of the school (point B). Every day he walks along the blocks to get to school. Because a large building occupies a blocks, he can only walk along the path shown in Figure 3‑10. If his route is as short as possible, how many different routes can he take?

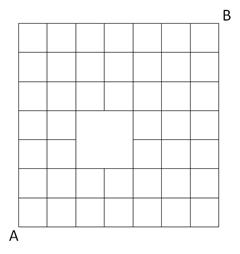
Figure 3‑10 Number of paths to school with blocked paths

Solution: The problem appears to be complex at first glance. The building creates a hole in the grid and makes the shape of the available blocks irregular. If we use a casework approach, we need to consider different scenarios on how a path first reaches the building. A much simpler approach is to add the streets removed by the building back, count the number of paths that include those “nonexistent” streets, and subtract the number from the total number of paths if the building were not there.

Following the last question’s logic, the total number of paths without the building is As shown in Figure 3‑11, to count the number of paths that include those “nonexistent” streets, the key is to recognize that all such paths include point C (the center of the building). Point C separates the paths to , which is a grid with combinations, and , which is grid with combinations. Therefore, the total number of paths to exclude is and the number of valid paths is

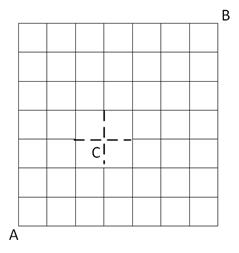
Figure 3‑11 Solution: Number of paths to school with blocked paths

««« Screwy pirates: A group of 11 pirates gathers together to put all the loot in a safe. Being a democratic bunch, they decide that only a majority – any majority – of them (≥6) together can open the safe. So they ask a locksmith to put a certain number of locks on the safe. To access the treasure, every lock needs to be opened. Each lock can have multiple keys, but each key only opens one lock. The locksmith can give more than one key to each pirate.

What is the smallest number of locks needed? And how many keys must each pirate carry?[12]

Solution: This problem is a good example of the application of combinatorial analysis in information sharing and cryptography. Let’s randomly select 5 pirates from the 11-member group; there must be a lock that none of them has the key to. Yet any of the other 6 pirates must have the key to this lock since any 6 pirates can open all locks. In other words, we must have a “special” lock to which none of the 5 selected pirates has a key, and the other 6 pirates all have keys. Such 5-pirate groups are chosen randomly. Thus, for each combination of 5 pirates, there must be such a “special” lock. The minimum number of locks needed is 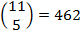locks.

Each lock has 6 keys, which are given to a unique 6-member subgroup. Therefore, each pirate must have keys. That’s surely a lot of locks to put on a safe, and a lot of keys for each pirate to carry.