Basic principle of counting and permutation

The rule of multiplication principle (also called the rule of products) is the basic rule of counting: When there are different events that are independent of each other, if there are possible outcomes for the first event, possible outcomes for the second event, …, and possible outcomes for the k-th event, then the total number of possible outcomes is

Let’s use a simple coin-tossing example and a tree diagram to explain the rule of multiplication. When we toss a fair coin, we get either a Head (H) or a Tail (T). If we toss a coin three times, what are the possible outcomes? As shown in Figure 3‑1, we have two possible outcomes for the first coin toss (H or T). For each outcome after the first toss, we get two possible outcomes with the second coin toss: H becomes HH or HT, and T becomes TH or TT. For each outcome after the second toss, we also get two possible outcomes with the third coin toss, which brings the total number of outcomes to

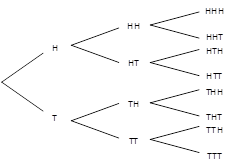
Figure 3‑1 Tree diagram for the rule of multiplication

Sometimes events happen over multiple steps, and the number of possible outcomes[10] of later steps may depend on the outcomes of earlier steps. We can use the generalized rule of multiplication: Let S be a set of length-k steps. If there are:

• possible first entries,
• possible second entries for each first entry,
• possible third entries for each combination of first and second entries, etc.

Then there are a total of possible outcomes. The key difference is that each step does not need to be independent. For example, a chess club of 50 members needs to elect a president and a vice president. In the first step, we choose the president, and there are 50 possible outcomes. In the second step, we choose the vice president from the remaining 49 members, and the number of possible outcomes is reduced to 49. The total number of possible outcomes is .

The generalized rule of multiplication is related to a key concept in counting called permutations. When we choose r objects from a group of n distinguishable objects sequentially, the ordered subset is called a permutation. For example, if we select 3 numbers from sequentially, is one permutation and is a different permutation as the order is different. In the chess club example, the order also matters. The outcome that A is elected president and B is elected vice president is different from the outcome that B is elected president and A is elected vice president.

The number of permutations is denoted as and can be calculated as

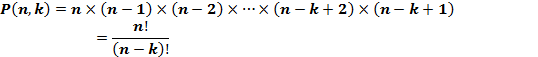
Let’s use the rule of multiplication and the number of permutations to solve some counting problems.

Part A. If a tiny library has 6 different books on a shelf. Each day a student randomly chooses a book to read, how many possible outcomes do we get after 6 days?

Part B. In how many ways can we arrange 6 different books on a shelf?

Solution: In part A, since we have 6 possible outcomes each day and there are 6 independent steps, the total number of possible outcomes is .

In part B, let’s arrange the books from left to right. There are again 6 steps in our selection. Unlike the steps in part A, each step is no longer independent. In the first step, there are 6 possible outcomes as we can choose one of the 6 books. In the second step, there are 5 possible outcomes as there are 5 books left. In the third step, there are 4 possible outcomes as there are 4 books left. Similarly, in the fourth, the fifth, and the sixth step, there are 3, 2, 1 possible outcome(s), respectively. Therefore, the number of possible arrangements is

The difference between these two problems lies in sampling with or without replacement. When we sample with replacement, each step is independent. If we begin with n choices, each step has n choices. What happens in one step has no impact on what happens in the next step. When we sample without replacement, each step is no longer independent. If we have n choices in the first step, we only have n-1 choices left in the second step.

How many integers between 1 and 1000 (inclusive) do not contain the digit 8?

Solution: We can express integers between 0 and 999 as where and are single digits For example, we express 71 as . There are 10 choices each for and If the integer does not contain the digit 8, there are 9 choices each for and Among the 1000 integers between 0 and 999, there are numbers that do not contain the digit 8. We need to exclude 0 and add 1000 back since we are counting the integers between 1 and 1000 that do not contain the digit 8. Therefore, the number of integers between 1 and 1000 that do not contain the digit 8 is 729.

A bookshelf has 4 math books, 3 chemistry books, and 2 biology books. They are all different.

Part A. How many ways can we arrange the books on the shelf if all chemistry books need to be kept together?

Part B. How many ways can we arrange the books on the shelf if all chemistry books need to be kept together and all biology books need to be kept together?

Solution: In part A, since we need to keep all the chemistry books together, let’s first treat all 3 chemistry books as 1 super chemistry book and arrange the super chemistry book with 4 math books and 2 biology books. There are possible permutations. Within the super chemistry book, we can arrange 3 chemistry books in possible ways. Therefore, the total number of ways is

We can apply the same logic to part B. Now there is 1 super chemistry book, 1 super biology book, and 4 math books. There are possible permutation. Within the super chemistry book, there are permutations; within the super biology book, there are permutations. Therefore, the total number of ways is

General Rule: When using permutations, if a subgroup of elements needs to stay together, they essentially become one element in the permutation with other elements. If the elements in the subset are indistinguishable, no additional multiplication is needed. If they are distinguishable, we need to multiply the number by the permutations within the group, which is