Factorials

The factorial of a nonnegative integer , denoted by , is the product of all integers from to . For example, .

Trailing zeros: How many trailing zeros are there in ?

Solution: We know that each pair of 2 and 5 will give a trailing zero. If we perform prime number decomposition on all the numbers in , it is obvious that the frequency of 2 will far outnumber the frequency of 5. Thus, the frequency of 5 determines the number of trailing zeros. Among numbers and 20 numbers are divisible by 5 (). Among these 20 numbers, 4 are divisible by 5² (). Therefore, the total frequency of 5 is 24, and there are 24 trailing zeros.

is an integer less than or equal to 25 and is not a multiple of How many possible values can have?

Solution: Since there is no obvious solution, let’s start by testing different values of

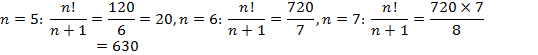
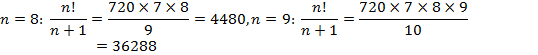
Now the pattern emerges: when is small , is not a factor of As becomes larger, is not a factor of if and only if is a prime number. Unless is a prime number, we can express it as the product of two numbers that are smaller than Possible values of are prime numbers (seven choices). Altogether, there are 10 numbers less than 25 that are not a multiple of