A geometric sequence is
a sequence of numbers where each term after the first is 
times
the previous term. The constant is called the common
ratio. For example, the sequence 
is a geometric sequence
that starts with 1 and ends with 256. The common ratio is
2. If the first term of a geometric sequence is 
and
the common ratio is , the n-th term in
the sequence is 
The summation of a
geometric sequence, 
is derived using the following analysis:
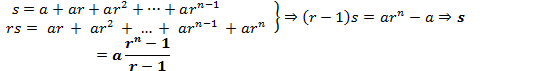
When 
, the value of 
converges towards 0 as 
increases
and the summation of the infinite geometric sequence, 
converges to 
:
if and 
and 
. We have 
.
For example, 
Problem 2‑39
Convert 0.234523452345… to fractions.
Solution: We can convert all repeating decimals to fractions. This question is just an example to show how to treat repeating decimals as the summation of an infinite geometric sequence to derive the fractions. Using the repeating pattern of 0.234523452345…, we can rewrite it as:
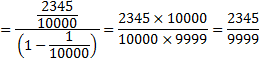
General Rule: We can always convert repeating decimals to fractions by treating the repeating part as the sum of an infinite geometric sequence.
Problem 2‑40
Let 
be the summation of the
geometric sequence 
be the
product of the sequence, and 
be the summation of
their reciprocals 
Prove that 
Solution: Using the summation formula, we have 
. 
How do we calculate ? If
we reverse the order of the elements in 
, we get 
which is again a
geometric sequence with a common ratio of .
The difference with the original sequence is that the first term is 
instead of 
Using
the same summation formula, we have 
and 
.
Therefore, 
Problem 2‑41
Calculate the sum 
Solution:
Let 
. If we multiply both
sides of the equation by 2, we get 
Therefore, 