Induction

Induction is similar to problem simplification. To solve a complex problem, it begins with simplified problems. Induction uses a mathematically well-defined process. It is one of the most powerful and commonly-used techniques in mathematics, especially discrete mathematics. Many problems that involve integers can be solved using induction. The general steps for proof by induction are the following:

• State that the proof/formula uses induction and define an appropriate predicate .
• Prove the base case , or any other smallest number n for the predicate to be true.
• Prove that implies for every integer n. Alternatively, in a strong induction argument, you prove that and together imply .

In most cases, the real difficulty lies not in the induction step, but to formulate the problem as an induction problem and come up with the appropriate predicate We usually start with the simplest versions of the problem—small n—to identify a pattern and estimate the formula. Then we use induction to prove that the same formula holds for all n’s.

What is the value of ?

Solution: The summation formula for consecutive squares is the following:

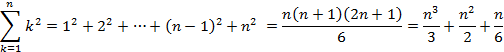
In case you do not remember the formula for the summation of squares, you only need to guess that the format of the equation is . Let’s apply the initial conditions to calculate and :

We will get . Since we already know that the formula works for and we only need to show if the formula works for , it works for as well.

Therefore, the formula works for and by induction, it works for any .

General Rule: and

Coin split problem: You split 1000 coins into two piles and count the number of coins in each pile. If there are x coins in pile one and y coins in pile two, you multiply x by y to get . Then you split both piles further, repeat the same counting and multiplication process, and add the new multiplication results to the original. For example, you split x to and , y to and , then the sum is . The same process is repeated until you only have piles of 1 coin each. What is the final sum? (The final 1’s are not included in the sum.)

Solution: Let n be the number of the coins and be the final sum. It is unlikely that a solution will jump to our mind since the number is large. If you are not sure how to approach the problem, it never hurts to start with the simplest cases and try to find a pattern. For this problem, the base case has . The only split is and the final sum is 1. When , the first split is and we have . The 2-coin pile will further give an extra multiplication result 1, so the final sum is 3. This analysis also provides the hint that when n coins are split into x and coins, the total sum will be . 4 coins can be split into or . For either case, we can apply and yields the same final sum 6.

Claim: For n coins, independent of intermediate splits, the final sum is . [26]

So how do we prove it? The answer should be clear: by induction. We have established the claim for the base cases . Assume the claim is true for coins, we need to prove that it holds for coins as well. Again we apply the equation . If N coins are split into x coins and coins, we have:

= .

Therefore, it holds for as well and is true for any . Applying the conclusion to , we have .

Part A. A rabbit sits at the bottom of a staircase with 8 stairs. The rabbit can hop up only one or two stairs at a time. How many different ways are there for the rabbit to ascend to the top of the stairs?[27] 

Part B. A rabbit sits at the bottom of a staircase with n stairs.  If the rabbit can hop up 1, 2, or 3 stairs at a time, how many different ways are there for the rabbit to ascend to the top of the stairs?

Part C. A rabbit sits at the bottom of a staircase with n stairs. If the rabbit can hop up 1, 3, or 4 stairs at a time, how many different ways are there for the rabbit to ascend to the top of the stairs?

Solution: For part A, let’s begin with the simplest cases and consider solving the problem for any number of stairs using induction. For , there is only one way and . For , we can have one 2-stair hop or two 1-stair hops. So . For any , there are always two possibilities for the last hop, either it’s a 1-stair hop or a 2-stair hop. In the former case, the rabbit is at before reaching n, and it has ways to reach . In the latter case, the rabbit is at before reaching n, and it has ways to reach . Thus, we have . Using this function we can calculate for The sequence as increases is [28]For the number of ways is 34.

The induction method is a general approach that works for different combinations of stairs per hop. In Part B, we again begin with the simplest cases. For , there is only one way and . For , we can have one 2-stair hop or two 1-stair hops. So . For there are four ways and . Starting from we can use the formula

Let’s again apply the same approach to Part C. For , there is only one way, and . For , we have two 1-stair hops. So . For there are two ways and . For there are four ways Starting from we can use the formula

«« Race track: Suppose that you are on a one-way circular race track. There are N gas cans randomly placed on different locations of the track, and the total sum of the gas in these cans is enough for your car to run exactly one lap of the track. Assume that your car has no gas in the gas tank initially, but you can put your car at any location on the track, and you can pick up the gas cans along the way to fill in your gas tank. Can you always choose a starting position on the track so that your car can complete the entire circle?[29]

Solution: If you get stuck as to how to solve the problem, again start with the simplest cases and consider using an induction approach. Without loss of generality, let’s assume that the circle has a circumference of 1. For , the problem is trivial. Just start at where the gas can is. For , The problem is still simple. Let’s use a figure to visualize the approach. As shown in Figure 4‑2 (A), the amount of gas in can 1 and can 2, expressed as the distance the car can travel, are and respectively, so The corresponding segments are and , so Since and we must have or ( and cannot both be true). If , we can start at gas can 1, which has enough gas to reach gas can 2, and get more gas from gas can 2 to finish the whole circle. Otherwise, we will just start at gas can 2 and pick up gas can 1 along the way to finish the whole circle.

The argument for also gives us a hint for the induction step. Now we want to show that if the statement holds for , then the same statement also holds for As shown in Figure 4‑2 (B), we have and for There must exist at least one that has . That means whenever the car reaches , it can reach with more gas (For , it goes to instead). In other words, we can actually combine and to one gas can at the position of with an amount of gas (and eliminate the gas can ). But such combination reduces the problem to , for which the statement holds. Thus, the statement also holds for Therefore, we can always choose a starting position on the track to complete the entire circle for any N.

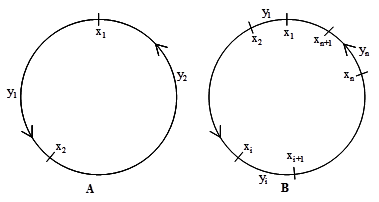
Figure 4‑2 Gas can locations on the cycle and segments between gas cans

There is also an alternative approach to this problem that provides a solution to the starting point. Let’s imagine that you have another car with enough gas to finish the circle. You put that car at the position of a randomly chosen gas can and drive the car for a full circle. Whenever you reach a gas can (including at the initial position), you measure the amount of gas in your gas tank before you add the gas from the can to your gas tank. After you finish the circle, read through your measurement records and find the lowest measurement. The gas can position corresponding to the lowest measurement should be your starting position if the car has no gas initially. It may take some thinking to understand this argument fully. We recommend that you draw a figure and give this argument some careful thoughts if you don’t find the reasoning obvious.