Least common multiple (LCM) & greatest common divisor (GCD)

For two positive integers and , the least common multiple (LCM) is the smallest positive number that is a multiple of both and . The greatest common divisor (GCD) is the biggest number that divides into both and . GCD is also called Greatest common factor (GCF). If we express as the product of GCD and another integer and as the product of GCD and another integer , we can derive the following formulas:

and are coprime (mutually prime) if the only positive integer (factor) that divides both of them is 1.

The definitions of GCD and LCM are not limited to two integers. For integers, LCM is the smallest positive number that is a multiple of all integers, and GCD is the biggest number that divides all integers.

One way to identify and is to use prime factorization:

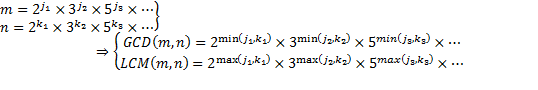
For example, to calculate the and of 24 and 180, let’s first find the prime factors of 24 and 180. Since and we can calculate the and using the formula:

The Euclidean Algorithm can be used to find

1.      If exchange and

2.      At each step, write in quotient remainder form (divide by to get and the remainder . If stop and report as the GCD.

3.      Replace by and replace by ; return to the previous step.

The key concept behind the Euclidean Algorithm is that where is an integer.

Let’s use the Euclidean Algorithm to find the GCD of and :

1.      Since exchange and

2.      Write in quotient remainder form

3.      Since replace by and replace by

4.      Repeat the quotient remainder step:

5.      Since we stop and report as the GCD.

Alternatively, we can simply write the steps of the Euclidean Algorithm as:

Part A. A positive integer leaves a remainder of 2 when divided by 8, 10, and 17. What is the smallest that is no smaller than

Part B. A positive integer leaves a remainder of 6 when divided by 8, a remainder of 8 when divided by 10, and a remainder of 15 when divided by 17. What is the smallest ?

Solution: For part A, let’s start with three simpler questions.

What is the smallest integer that leaves a remainder of 2 when divided by 8, 10, and 17? It is 2.

What is the smallest positive integer that leaves a remainder of 0 when divided by 8, 10, and 17? It is their least common multiple:

What is the pattern of an integer that leaves a remainder of 2 when divided by 8, 10, and 17? It is where a nonnegative integer.

Therefore, the smallest that leaves a remainder of 2 when divided by 8, 10, and 17 and is no smaller than is

Part B is a little more complex. We no longer have the same remainder for all the divisors. The remainders still have a pattern: . In other words, if we increase by 2, it will be divisible by and . What are the numbers that are divisible by and Their common multipliers, The integer numbers in series , where a positive integer, leaves a remainder of 6 when divided by 8, a remainder of 8 when divided by 10, and a remainder of 15 when divided by 17. The smallest one is

General Rules: Positive integers that leave a remainder of when divided by are the series where a nonnegative integer.

Positive integers that leave a remainder of when divided by a remainder of when divided by …, and a remainder of when divided by are the series where a positive integer.

What is the ratio of the least common multiple of 180 and 594 to the greatest common factor of 180 and 594?

Solution: First, let’s solve the problem by prime factorization.

We can also directly use the relationship between LCM and GCD.

Because a number is divisible by 9 if the sum of its digits is divisible by 9, we can identify both numbers as multiples of 9. Both are also even numbers, so they are divisible by 2, and their GCD is at least 18. If we divide 180 and 594 by 18, we get 10 and 33.

,

Since the GCD of 10 and 33 is 1, we know that 18 is indeed the GCD of 180 and 594. Therefore, the ratio of their LCM to GCD is and

Last, let’s also try using the Euclidean Algorithm to identify

1. Make by exchanging the numbers: ,

2. Divide by : quotient remainder

3. Replace by and by :

4. Divide by : quotient remainder

5. Replace by and by :

6. Divide by : quotient remainder

Since we stop and report as the GCD.

Part A. If are integers, which of the following cannot be the value of

(A) 4 (B) 312 (C) 2578 (D) 3520 (E) 780

«« Part B. If are integers, find a pair of that makes

Solution: Since and must be a multiple of as well. Among the choices, is not a multiple of as is not a multiple of . The answer to Part A is C.

General Rule: be four integers numbers and . must be a multiple of . The reason is intuitive: Since is a multiple of and is a multiple of and are all multiples of

For part B, the problem is equivalent to finding the that makes . If we apply the Euclidean Algorithm, we will get for and . The process also provides a way to identify pair that makes . Let’s track each step and express the remainder as a linear combination of and

Therefore, and . Let’s verify the results: . is not the only answer for Since any with the pattern where is an integer, also works. Let’s again verify the result:

General Rule: The Linear Equation Theorem gives the general solution to such problems. Let and be nonzero integers and The equation always has a solution that can be found in the Euclidean Algorithm method. All solutions to the equation can be obtained by the formula . All integers that are multiples of can be expressed as a linear combination of and as well.

A palindromic number is a number that remains the same when its digits are reversed (e.g., 4554). What is the largest 4-digit palindromic number that is the product of two 2-digit integers?

Solution: The key to solve this problem is to recognize that 4-digit palindromic numbers are multiples of 11. Let represent a 4-digit palindromic number, we have which satisfies the condition for a number to be divisible by 11. The biggest 2-digit number that is a multiple of 11 is 99. The largest 4-digit palindromic numbers are Are any of them multiples of 99? To be a multiple of 99, needs to be a multiple of 9 as the sum of the 4 digits needs to divisible by 9. 9009 and 9999 satisfy the requirements. Does 9999 work? ; it is no longer the product of two 2-digit integers. The largest number that is the product of two 2-digit integers is . Therefore, the largest 4-digit number that is the product of two 2-digit integers is 9009.

«« What is the smallest 5-digit palindromic number that is a multiple of 99?

Solution: Let represent a 5-digit palindromic number. For the number to be a multiple of 9, must be multiple of 9; for the number to be a multiple of 11, must be a multiple of 11. Let and where is a positive integer and is an integer, which also means that . Since must be a multiple of and must both be odd numbers or both be even numbers. and are the smallest combination to make both even; and are the smallest combination to make both odd.

which is not a multiple of

which is a multiple of and

Thus, We want to make as small as possible, which makes as small as possible. The largest possible value for a digit is When Therefore, the smallest 5-digit palindromic number that is a multiple of 99 is 54945.

A different approach may make the results more intuitive. We know that are multiples of and can remove such multiples from the calculation:

If is a multiple of needs to be a multiple of The smallest possible sum for is itself. Since must be (If if ). When Again, we get Therefore, the smallest 5-digit palindromic number that is a multiple of 99 is 54945.