Magic squares

A magic square is a square filled with distinct positive numbers such that the sum of the integers in each row, column, and diagonal is equal. The sum is called the magic constant. As shown in Figure 2‑2, the magic square can be traced back to HetuLuoshu (河图洛书), a collection of ancient Chinese diagrams that are more famous for the first chart of Ying and Yang. In the traditional definition of a magic square, the numbers in the squares are natural numbers Such a magic square is also called normal magic square. Math problems use a generalized version of magic squares. They allow numbers to be different from

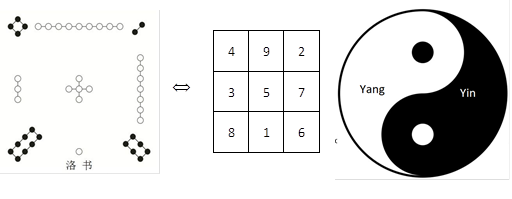
Figure 2‑2 Magic square and Yin-Yang chart from HetuLuoshu

Figure 2‑3 shows a generalized version of 3 × 3 magic square.

Figure 2‑3 Generalized version of a magic square

Equation (1) to equation (8) show the expressions for the sums of rows, columns, and diagonals. The sums are all equal to the magic number .

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

Let the sum of all numbers, be S, we can derive the following properties from the equations:

1.      magic constant (sum of equation 1, 2, 3 shows

2.      (sum of equation 2, 5, 7, 8 shows )

3.     

4.      (the sum of equation 4 and 7 equals the sum of equation 2 and 3: ).

Similarly, we have and

The number at the center of the square must be the average of the 9 numbers. Each row, column, or diagonal adds up to 3 times the average. The number at the corner of the square is the average of the two numbers that are not in the same row, column, or diagonal of that number.

In general, the magic number in an magic square is the average of the input numbers times This follows from the equation that the sum of rows (or columns) is the sum of all input numbers.

In the following square, the sum of the numbers in each row, column, and diagonal are equal. What is ?

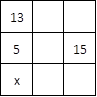
Solution: In this problem, 3 numbers are given. When these 3 numbers are not all in the same row, column, or diagonal, all numbers in the square can be determined. Figure 2‑4 shows how to calculate the remaining numbers. Since the sum of the first column is The sum of all three rows, three columns, and two diagonals must be In the second row, the number in the center of the square must be In the top-left to bottom-right diagonal, the number at the bottom right must be 7. In the last column, the number in the first row must be Now we have sufficient information to calculate as We can go ahead to fill in the rest of the numbers and verify that the sum of each row, column, and diagonal is equal to 30.

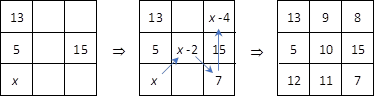
Figure 2‑4 Derivation of a 3×3 magic square

In the following square, the sums of the numbers in each row, column, and diagonal are equal. What is ?

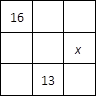
Solution: The number at the corner of the square is the average of the two numbers that are not in the same row, column, or diagonal of that number. Therefore, and

In the following square, the sums of the numbers in each row, column, and diagonal are equal. What is ?

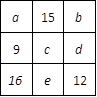
Solution: Since we have The number at the corner of the square is the average of the two numbers that are not in the same row, column, or diagonal of that number:

In the following magic square, the sums of the numbers in each row, column, and diagonal are equal. The numbers in the squares are What is ?

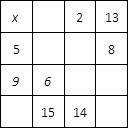
Solution: The average of the numbers is Since the magic number in an magic square is the average of the input numbers times each row, column, and diagonal adds up to Using this observation, we can fill in all the remaining cells in the square as expressions of (Figure 2‑5). Since the sum of the top-left to bottom-right diagonal is also 34, we can calculate using the following equation:

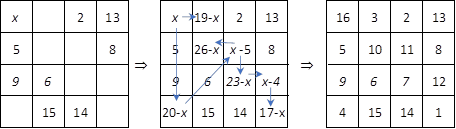
Figure 2‑5 Derivation of a 4×4 magic square