Modular arithmetic

The modulo operation—denoted as or —finds the remainder () of division of number by .[5] For example, or

Modular addition:

Modular subtraction:

Modular multiplication:

Modular exponentiation:

If and leave the same remainder when divided by (), and are congruent (or equivalent) modulo . We express it as .[6] If and are not congruent modulo b, we express it as

If and is the modulo-b residue of .

If and .

If and .

If and .

If and .

If for any positive integer .

Some general observations from modular operations:

·         If

·         are all different numbers.

·         If for any integer In other words, if

·         Modular operations apply to negative integers.

The square of any odd number and 1 are congruent modulo 8. If we express an odd number as where is an integer, then Since is always an even number, is divisible by 8. Therefore, .

Fermat’s little theorem: If is a prime number, for any integer is an integer multiple of

Wilson’s theorem: a positive integer is a prime number if and only if the product of all positive integers less than is one less than a multiple of In other words, is a prime number if and only if

What is the remainder of the division of by 7?

Solution: Let’s combine modular exponentiation, modular multiplication, and modular addition to solve this problem. First, let’s decompose to . Why do we want to express most of the terms using 8? Because . Thus, we have . Since using modular multiplication, we get . Using modular addition, we get .

General Rule: A general approach is to find then we can take advantage of and to get

What is the remainder of the division of by ?

Solution: We can use the same technique as the last problem. Since and and . We have and .

Therefore and the remainder of the division of by 11 is 0.

Since modular operations apply to negative integers, a simpler solution is to use and :

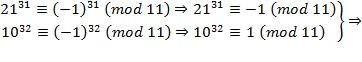
Therefore, the remainder of the division of by 11 is 0.

Which of the following is a perfect square?

(A) 34567 (B) 21089 (C) 16129 (D) 54315 (E) 42102

Solution: We know that the square of any odd number and 1 are congruent modulo 8. In other words, when we divide a perfect square that is odd by 8, the remainder must be 1. To calculate the remainder if we divide a number by 8, we only need to examine the remainder of the last 3 digits. For example, Since and they cannot be perfect squares. Since and they may be perfect squares. To check whether 20189 or 16129 is a perfect square, we can either do so through trial and error or using more modular rules. If you are familiar with algebra, you may have recognized that and It is easy to see that Therefore, 21089 cannot be a perfect square.

Let’s also try the route of using more modular rules. When we derived that the square of any odd number and 1 are congruent modulo 8, we used the remainder of a number divided by 8. If we divide a number x by 3, the remainder we get is 0, 1, or 2:

Therefore, if we divide a perfect square by 3, the remainder must be 0 or 1. Since it cannot be a perfect square. Therefore, the answer is (C) 16129. We can verify that .

General Rule: When we divide a perfect square by 3, the remainder must be 0 or 1.

December 31, 2019 is a Tuesday. What day of the week is December 31, 2029?

Solution: Problems on day of the week are problems about the remainder if we divide the day by 7. A common year has 365 days and A leap year has 366 days and Each common year has 52 weeks and 1 extra day, and each leap year has 52 weeks and 2 extra days. There are 10 years between December 31, 2019, and December 31, 2029; 3 of the 10 years are leap years (2020, 2024, 2028). There are 13 extra days in total. Therefore, the day of the week of December 31, 2019, is 6 days after Tuesday (or 1 day before Tuesday), which is a Monday.

General Rule: The day of the week increases by 1 for each common year and increases by 2 for each leap year.

A bag has 20 blue balls and 14 red balls. Each time you randomly take two balls out. (Assume each ball in the bag has an equal probability of being taken). You do not put these two balls back. Instead, if both balls have the same color, you add a blue ball to the bag; if they have different colors, you add a red ball to the bag. Assume that you have an unlimited supply of blue and red balls. If you keep on repeating this process, what will be the color of the last ball left in the bag?[7] What if the bag has 20 blue balls and 13 red balls instead?

Solution: Once you understand the hint, this problem should be an easy one. Let represent the number of blue balls and red balls in the bag. We can take a look at what will happen after two balls are taken out.

Both balls are blue:

Both balls are red:

One red and one blue:

Note that R either stays the same or decreases by 2. Thus, the number of red balls will never become odd if we begin with 14 red balls. We also know that the total number of balls decreases by one each time until only one ball is left. Combining the information that we have, the last ball must be a blue one. Similarly, when we start with an odd number of red balls, the final ball must be a red one. Therefore, if we start with 20 blue balls and 13 red balls, the last ball is red.

««« Chameleon colors: A remote island has three types of chameleons with the following population: 13 red chameleons, 15 green chameleons, and 17 blue chameleons. Each time two chameleons with different colors meet, they would change their colors to the third color. For example, if a green chameleon meets a red chameleon, they both change their color to blue. Is it ever possible for all chameleons to become the same color? Why or why not?[8]

Solution: It is not possible for all chameleons to become the same color. For all the chameleons to become the same color, at a certain intermediate stage, two colors must have the same number. To see this, just imagine the stage before the final stage. It must have a combination of . For chameleons of two different colors to have the same number, their module of 3 must be the same as well. We start with and chameleon, when two chameleons of different colors meet, we will have three possible scenarios:

Therefore, the pattern is preserved, and we will never get two colors to have the same module of 3. In other words, we cannot make two colors have the same number. Therefore, the chameleons cannot become the same color. Essentially, the relative change of any pair of colors after two chameleons meet is either 0 or 3. In order for all the chameleons to become one color, at least one pair’s difference must be a multiple of 3.

[5] In math books, you are far more likely to see instead of . Many of the popular programming languages (e.g., C++, Javascript, Python) use as the modulo operation.

[6] We need to pay attention to the difference between and is an equivalence relation and can take many values; is an equality. is the smallest positive solution to the equation