Thinking outside the box

Real-life problems are usually not standard textbook problems. Solving difficult problems sometimes requires a little bit of creativity to look at the problem from a new perspective and solve the problem using nonstandard approaches. In this section, let’s use several examples to demonstrate how out-of-the-box thinking leads to insightful and fast solutions.

A chocolate bar has 6 rows and 8 columns (48 small squares). You break it into individual squares by making a number of breaks. Each time, break one rectangle into two smaller rectangles. For example, in the first step, you can break the chocolate bar into a one and a one. What is the total number of breaks needed to break the chocolate bar into 48 small squares?Solution: The problem may look like a complex one. There are so many ways to break the chocolate bar, and each piece can be further broken in many ways. What is the key to solving this problem? Instead of focusing on different possible ways to break a bar at each step, each break shares the same property: the number of pieces always increases by 1 with each break since it always breaks one piece into two. In the beginning, we have a single piece. In the end, we will have 48 pieces. Therefore, the number of breaks must be .

Problem 4‑10

You have an chessboard with two small squares at the opposite diagonal corners removed. You have many bricks with dimension Can you pack 31 bricks into the remaining 62 squares?

Solution: This is a popular chessboard problem. A real chess board figure surely helps the visualization. As shown in Figure 4‑1, when a chess board is filled with alternative black and white squares, both squares at the opposite diagonal corners have the same color. If you put a brick on the board, it will always cover one black square and one white square. Let’s say it’s the two black corner squares are removed, then the rest of the board can fit at most 30 bricks since we only have 30 black squares left (and each brick covers one black square). To pack 31 bricks is out of the question. To cover all 62 squares without overlapping or overreaching, we must have exactly 31 bricks. Yet we have shown that 31 bricks cannot fit into the 62 squares left. Therefore, we cannot pack 31 bricks into the remaining 62 squares.

Figure 4‑1 Chessboard with alternative black and white squares

«« Box packing: Can you pack 53 bricks of dimensions into a box?

Solution: This problem is similar to the previous one. If we look at the total volume in this 3D problem, 53 bricks have a volume of 212, which is smaller than the box’s volume 216. Yet we can show it is impossible to pack all the bricks into the box using a similar approach as the chessboard problem. Let’s imagine that the box is actually comprised of small cubes. There should be 27 small cubes. Similar to the chessboard (but in 3D), imagine that we have alternating black and white cubes—it does take a little 3D visualization. Thus, we have either 14 black cubes & 13 white cubes or 13 black cubes & 14 white cubes. For any brick that we pack into the box, half () of it must be in a black cube, and the other half must be in a white cube. 53 bricks of dimensions have a half of their volume in white cubes and a half in black cubes; the minimum volume needed for all the white cubes combined is , and the same value is needed for the black cubes. But for the color with 13 cubes, be it black or white, the total volume is , which is less than 106. Therefore, we cannot pack 53 bricks of dimensions into a box.

Calendar cube: You just had two dice custom-made. Instead of numbers 1-6, you place single-digit numbers on the faces of each dice so that every morning you can arrange the dice in a way as to make the two front faces show the current day of the month. You must use both dice (in other words, days 1-9 must be shown as 01-09), but you can switch the order of the dice if you want. What numbers do you have to put on the six faces of each of the two dice to achieve that?

Solution: Since the days of a month include 11 and 22, both dice must have 1 and 2. To express single-digit days, we need to have at least a 0 in one dice. Let’s put a 0 in dice one first. Considering that we need to express all single-digit days and dice two cannot have all the digits from 1 – 9, it’s necessary to have a 0 in dice two as well in order to express all single-digit days.

So far, we have assigned the following numbers:

If we can assign all the rest of digits 3, 4, 5, 6, 7, 8, and 9 to the rest of the faces, the problem is solved. But there are 7 digits left. What can we do? Here’s where we need to think outside the box. We can use a 6 as a 9 since they will never be needed at the same time! Therefore, simply put 3, 4, and 5 on one dice and 6, 7, and 8 on the other dice, and the final numbers on the two dice are:

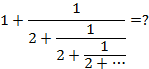
Solution: Let be the original expression. Then, we have:

What is the value of ?

Solution: We can again apply the last problem’s approach. Let , then we have Since must be positive, we have

There is a light bulb inside a room and four switches outside. All switches are currently at an off state, and only one switch controls the light bulb. You may turn any number of switches on or off any number of times you want. How many times do you need to go into the room to figure out which switch controls the light bulb?

Solution: Whether the light is on and off is binary, which only allows us to distinguish two switches. If we have another binary factor, there are possible combinations of scenarios, and we can distinguish 4 switches. Besides light, a light bulb also emits heat and becomes hot after the bulb has been lit for some time. Therefore, we can use the on/off and cold/hot combination to decide which one of the four switches controls the light.

Turn on switches 1 and 2; move on to solve some math problems; turn off switch 2 and turn on switch 3; get into the room quickly, touch the bulb and observe whether the light is on or off.

The light bulb is on and hot → switch 1 controls the light;

The light bulb is off and hot → switch 2 controls the light;

The light bulb is on and cold → switch 3 controls the light;

The light bulb is off and cold → switch 4 controls the light.