The principle of overcounting

The principle of overcounting counts in a two-step procedure:

1.      Use a “wrong” approach to count that yields a number that is too high.

2.      Figure out how “wrong” the number is and reduce it to the correct number (often by division or subtraction).

Let’s use some examples to show how to apply the principle of overcounting.

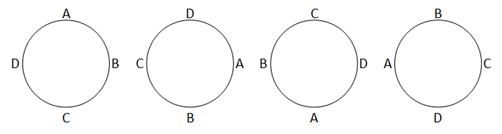
How many ways can we arrange 4 people at a table? Two arrangements are the same if one arrangement can be rotated to look like the other (they are rotationally symmetric). For example, all four seating arrangements in Figure 3‑2 are considered to be the same.

Figure 3‑2 Equivalent sitting arrangements

Solution: There are two ways to address the overcounting caused by rotational symmetry. One way is to use the principle of overcounting. First, we use a “wrong” approach to count all permutations, which gives us Then we correct the overcounting: Since every 4 sitting arrangements can be rotated to look alike, we need to divide the “wrong” number by 4. Therefore, the number of arrangements is

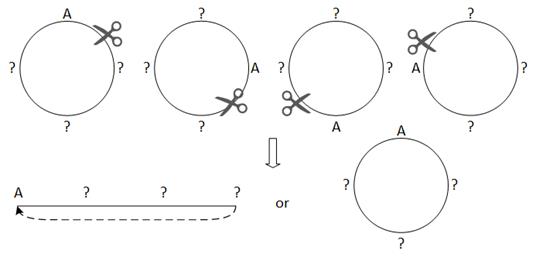
Figure 3‑3 Equivalent sitting arrangements

Another way is to place one of the people to fix the rotation and convert it to a common permutation problem. As shown in Figure 3‑3, after we place A, we can cut the circle (table) and convert the problem to a linear seating problem. Now it is clear that the problem is to choose 3 people from 3 people sequentially and the number of permutations is Alternatively, we can fix A at a specific position on the table and then assign seats to the other 3 people. Again, the number of permutations is When we use the approach of cutting the circle and converting it to a linear seating problem, we need to remember that the seat at the end of the row is a neighboring seat of A’s seat. For that reason, we add a dotted line back to A.

General Rule: When we count the ways of arranging items around a circle, we can use two approaches:

· Overcount the arrangements first and then correct the overcounting caused by rotational symmetry.

· Fix the location of one item on the circle to convert the problem to a linear problem.

Note that rotational symmetry is not limited to a circle. We also need to consider rotational symmetry when arranging items around any regular polygons (e.g., square).

A round table has 8 seats. In how many ways can we place 8 people around the table if two of the people, Alex and Jack, refuse to sit together?

Solution: Let’s use the approach of assigning a seat to one person to convert the problem to a linear seating problem. Let’s assign Alex a seat first and calculate the arrange for the following linear seating:

We need to assign 7 people to a row of 7 seats. Since Jack cannot sit together with Alex, he cannot sit at either seat 1 or seat 7 (remember that seat 7 is a neighboring seat of Alex’s). There are 5 choices for Jack; the number of arrangements for the other 6 people is Therefore, the number of arrangements is .

We can also solve the problem using complementary counting. If there is no restriction, the total number of arrangements is We need to exclude the cases that Alex and Jack sit together. First, they are treated as one person along with the other 6 people around the table, and we have arrangement. Since Alex and Jack are distinguishable, we multiply the number by the permutations within the group, which is Therefore, the number of cases that Alex and Jack sit together is and the number of cases that Alex and Jack do not sit together is .

In how many ways can the letters in the word BANANA be arranged?

Solution: The word BANANA has 6 letters: 3 As, 2 Ns, and 1 B. First, let’s overcount: there are permutations for 6 letters. Then, let’s correct for the overcounting. There are 3 As. let’s label them as and There are permutations of and :

In the overcounting part, they are counted as 6 different permutations. Since the 3 As are alike (indistinguishable), all 6 permutations are the same To correct for the overcounting, we need to divide the count by Similarly, the 2 Ns are alike; we correct for the overcounting by dividing into the count. Therefore, the number of arrangements are .

General Rule: There are different permutations of items, of which items are alike, items are alike,…, items are alike (the items of different groups are different).

Part A. In how many ways can the letters in the word TOMATO be arranged?

Part B. A bookshelf has 6 identical math books, 2 identical chemistry books, and 2 identical biology books. In how many ways can we arrange the books?

Solution: For part A, the word TOMATO has 6 letters: 2 Ts, 2 Os, 1 M, and 1A. We are arranging 6 items, of which 2 Ts are alike, 2 Os are alike, 1 M is alike, and 1 A is alike.

Therefore, the number of ways to arrange the letters in TOMATO is .

For part B, we are arranging 10 items, of which 6 math books are alike, 2 chemistry books are alike, and 2 biology books are alike.

Therefore, the number of ways to arrange the books on the shelf is

Now, you should see that no matter what the items are, the approach to handle indistinguishable items is the same.