or 
Pascal's Identity is a combinatorial identity about binomial coefficients:
or
We can prove the equation by expanding the formula for 
choose
and choose
:
Let’s consider the intuition behind the equation. The left-hand
side chooses a subset of items from 
items.
There are two possible cases:
·
The first item is not chosen: We need to choose items
from the remaining items, which has 
combinations.
·
The first item is chosen: We need to choose items
from the remaining items, which has 
combinations.
The total number of combinations is 
and 
Figure 3‑12 shows Pascal’s Triangle. The elements
on the left and the right edges of the Pascal’s Triangle are 
. The
rest of the elements are calculated using the same rule: each element is the
sum of the two elements above it. For example, the 3rd element in line 4 is the
sum of the 2nd element in line 3 and the 3rd element in line 3: 
Figure 3‑12 Pascal’s Triangle
As shown in Figure 3‑13, the k-th element in line
n of the Pascal’s Triangle, where 
is the number of
combinations of n distinct items taken at a
time, 
This is the result of
how each element is calculated: When 
or 
its
value is 
When is
between 1 and n, it is the sum of the two elements above the k-th
element in line n, 
and 
Using Pascal’s Identity,
we get the k-th element in line n as 
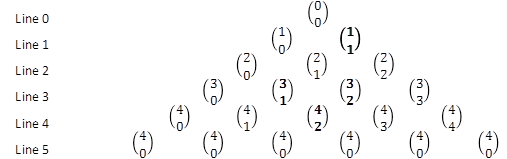
Figure 3‑13 Elements in Pascal’s Triangle
Problem 3‑28
Prove the Hockey Stick Identity: 
Solution:
The key to the proof is to recognize 
. Once we replace the
first term on the right-hand side as 
we can repeatedly apply
Pascal’s Identity:
