The pigeon hole principle

The basic version of the Pigeon Hole Principle states that, if you have fewer pigeon holes than pigeons and you put every pigeon in a pigeon hole, then at least one pigeon hole has more than one pigeon. In other words, it says that if you have holes and at least pigeons, at least 2 pigeons have to share one of the holes. The generalized version states that, if you have holes and at least pigeons, then at least pigeons have to share one of the holes. These simple and intuitive ideas are surprisingly useful in many problems. Here we will use some examples to show their applications.

Matching socks: Your drawer contains 2 red socks, 20 yellow socks, and 31 blue socks. Being a busy and absent-minded student, you just randomly grab some socks out of the drawer and try to find a matching pair. Assuming that each sock has an equal probability of being selected, what is the minimum number of socks you need to grab to guarantee a pair of socks of the same color?

Solution: This question is just a variation of the even simpler version of the two-color-socks problem, in which case you only need 3. When you have 3 colors (3 pigeon holes), by the pigeon hole principle, you will need to have socks (4 pigeons) to guarantee that at least two socks have the same color (2 pigeons share a hole).

AMC10-2006-20 Six distinct positive integers are randomly chosen between 1 and 2006, inclusive. What is the probability that some pair of these integers has a difference that is a multiple of 5?

(A) 1/2 (B) 3/5 (C) 2/3 (D) 4/5 (E) 1

Solution: We know that the difference of two integers is divisible by 5 if they have the same remainder when they are divided by 5. When a number is divided by 5, the possible remainders are 0, 1, 2, 3, 4. Since there are 5 possible remainders and 6 integers, at least two of them must have the same remainder when they are divided by 5. Therefore, we can always find a pair that has a difference that is a multiple of 5; the probability is 1.

You are invited to a welcome party with 25 fellow team members. Each of the fellow members shakes hands with you to welcome you. Since some people in the room haven’t met each other, there’s a lot of random handshaking among others as well. If you don’t know the total number of handshakes, can you say with certainty that there are at least two people present who shook hands with exactly the same number of people?

Solution: There are 26 people at the party. Each shakes hands with 1—since everyone shakes hands with you—to 25 people. In other words, there are 26 pigeons and 25 holes. As a result, at least two people must have shaken hands with exactly the same number of people.

Show me that, if there are 6 people at a party, then either at least 3 people met each other before the party, or at least 3 people were strangers before the party.

Solution: This question appears to be a complex one. But once you start to analyze possible scenarios, the answer becomes obvious.

Let’s say that you are the 6th person at the party. Then by generalized Pigeon Hole Principle, among the remaining 5 people, we conclude that either at least 3 people met you or at least 3 people did not meet you. Now let’s explore these two mutually exclusive and collectively exhaustive scenarios:

Case 1: Suppose that at least 3 people met you before.

If two people in this group met each other, you and the pair (3 people) met each other. If no pair among these people met each other, then these people ( people) did not meet each other. In either sub-case, the conclusion holds.

Case 2: Suppose at least 3 people did not meet you before.

If two people in this group did not meet each other, you and the pair (3 people) did not meet each other. If all pairs among these people knew each other, then these people ( people) met each other. Again, in either sub-case, the conclusion holds.

Therefore, at least 3 people met each other before the party, or at least 3 people were strangers before the party.

Ants on a square: There are 51 ants on a square with a side length of 1. If you have a glass with a radius of 1/7, can you put your glass at a position on the square to guarantee that the glass encompasses at least 3 ants? [20]

Solution: To guarantee that the glass encompasses at least 3 ants, we can separate the square into 25 smaller areas. Applying the generalized Pigeon Hole Principle, we can show that at least one of the areas must have at least 3 ants. Thus, we only need to make sure that the glass is large enough to cover any of the 25 smaller areas. Simply split the area into smaller squares with a side length of 1/5 each will do since a circle with a radius of 1/7 can cover a square[21] with a side length 1/5.

Counterfeit coins: There are 5 bags with 100 coins in each bag. A coin can weigh 9 grams, 10 grams, or 11 grams. Each bag contains coins of equal weight, but we do not know what type of coins a bag contains. You have a digital scale (the kind that tells the exact weight). How many times do you need to use the scale to determine which type of coin each bag contains? [22]

Solution: If the answer for 5 bags is not obvious, let’s start with the simplest version of the problem—1 bag. We only need to take one coin to weigh it. Now we can move on to 2 bags. How many coins do we need to take from bag 2 to determine the coin types of bag 1 and bag 2? Considering that there are three possible types for bag 1, we will need three coins from bag 2; two coins won’t do. For notation simplicity, let’s change the number/weight for three types to -1, 0, and 1 (by removing the mean of 10). If we only use 2 coins from bag 2, the final sum for 1 coin from bag 1 and 2 coins from bag 2 ranges from -3 to 3 (7 pigeon holes). At the same time, we have 9 () possible combinations for the weights of coins in bag 1 and bag 2 (9 pigeons). So at least two combinations will yield the same final sum (9>7, so at least two pigeons need to share one hole), and we cannot distinguish them. If we use 3 coins from bag 2, then the sum ranges from -4 to 4, which is possible to cover all 9 combinations. The following table shows that all possible combinations yield different sums:

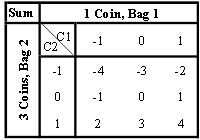
C1and C2 represent the weights of coins from bags 1 and 2, respectively.

Then how about 3 bags? We are going to have possible combinations. Surely an indicator ranging from – 13 to 13 will cover it, and we will need 9 coins from bag 3. The following table shows the possible combinations:

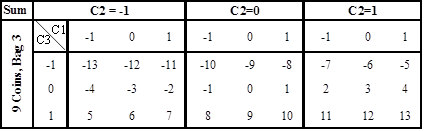
C1, C2, and C3 represent the weights of coins from bags 1, 2, and 3, respectively.

Following this logic, it is easy to see that we will need 27 coins from bag 4 and 81 coins from bag 5. Therefore, the answer is to take 1, 3, 9, 27, and 81 coins from bags 1, 2, 3, 4, and 5, respectively, to determine which type of coins each bag contains using a single weighing.