Union and intersection

A set is a collection of distinct objects. A universal set, also called the universe, is the set of all objects under consideration for a particular problem. Typically, is used to represent the universe. If the set has many elements, we can define the values specified by its conditions after a vertical bar. For example, is a set. The vertical bar means “such that.” If a set has only a few elements, we can directly list all elements in a pair of curly braces. For example, a roll of a dice has 6 possible outcomes: 1, 2, 3, 4, 5, 6. Let’s define and set as all the odd numbers in the universe: . If an object is in a set, it is an element of the set. The symbol indicates set membership and means “is an element of.” We have and

The complement of a set , is the set that contains all the elements not in .

The union of two sets and , is the set that contains all of the elements that are in either or (or both).

The intersection of two sets and , , is the set that contains all of the elements that are in both and .

The difference of sets and , is the set of elements in but not in

The complement of is . Let’s define as all the numbers in the universe (of outcomes of a dice roll) that are larger than 3, Then the union of and is the intersection is the difference is

Two sets are mutually exclusive if where is an empty set. and are always mutually exclusive.

If all elements of are elements of then is a subset of and we denote the subset relationship as is read as “subset or equal to,” as may have the same number of elements as If has fewer elements than is a proper subset of and we denote the relationship as

The principle of inclusion and exclusion (PIE) gives a formula for the number of elements in the union of and If is the number of elements in and is the number of elements in , then the number of elements in the union , is the sum of and minus the number of elements in the intersection of A and B :

The Venn Diagram shows why the formula holds. When we sum the number of elements in and the number of elements in , we count the elements in the intersection of and twice. Therefore, we need to remove the double counting to get the number of elements in the union of and .

Figure 3‑14 Venn diagram of two sets

De Morgan’s laws:

Assume that 200 students take the AP (Advanced Placement) chemistry class and 250 students take the AP biology class.

Part A. How many students, in total, take Biology and/or Chemistry if 50 students take both classes?

Part B. How many students take both classes if 370 students take either the AP chemistry class or the AP biology class, or both?

Solution: For part A, we can apply the PIE equation Let A represent the students who take the AP chemistry class in a high school, and B represent the students who take the AP biology class in the same high school. The union of A and B, represents the students who take either the AP chemistry class or the AP biology class. The intersection of A and B, represents the students who take both AP chemistry and AP biology.

Let’s explain the intuition behind the solution using the following Venn diagram:

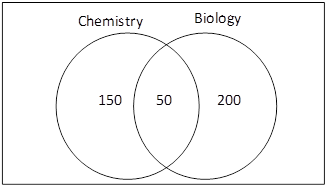
Figure 3‑15 Venn diagram of AP classes

Since 200 students take the AP chemistry class and 50 of them also take the AP biology class, 150 students take only the AP chemistry class. Since 250 students take the AP biology class and 50 of them also take the AP chemistry class, 200 students take only the AP biology class. Therefore, the number of students who take either class or both can be calculated as:

Students who take only chemistry + students who take only biology + students who take both =

For the second question, we can again apply the PIE equation :

Let’s explain the intuition behind the solution using the following Venn diagram:

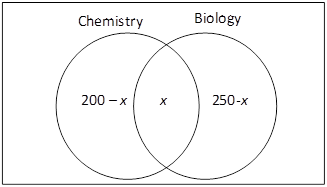
Figure 3‑16 Venn diagram of AP classes

Let’s assume that x students take both classes. The number of students who take only the AP chemistry class is . The number of students who take only the AP biology class is . Therefore, the number of students who take either class or both can be calculated as:

Students who take only chemistry + students who take only biology + students who take both

=

General Rule: Use a Venn Diagram when solving problems involving unions and interactions of sets.

Now let’s expand to three sets. The union of three sets A, B, and C, is the set that contains all of the elements that are in A, B or C. The intersection of the three sets, , is the set that contains all of the elements that are in A, B, and C. For three sets, the principle of inclusion and exclusion becomes:

The Venn Diagram in Figure 3‑17 again shows why the formula holds. When we sum the number of elements in A, B, and C, we double count the elements in the subset represented by AB2, AC2, and BC2, and triple count the elements in ABC3. To correct the overcounting, we need to deduct and once and twice.

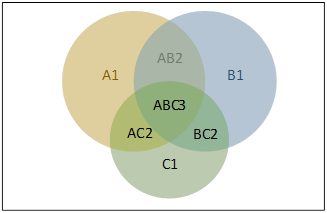
Figure 3‑17 Venn Diagram of three sets

From the diagram, we also have the following observations.

Therefore, we can calculate the elements in as:

Part A. is an integer among If is not a multiple of or how many possible values can take?

Part B. If is a multiple of 3 or 4 but not a multiple of 6, how many possible values can take?

Solution: In this problem, we combine the principle of inclusion and exclusion with complementary counting. Instead of counting the number of integers that are not a multiple of 3, 4, or 5, we can count the numbers that are a multiple of 3, 4, or 5 first. Let be the set of the integers that are divisible by 3, be the set of the integers that are divisible by 4, and be the set of the integers that are divisible by 5. and are the sets of the integers divisible by 12, 15, and 20, respectively. is the set of the integers that are divisible by 60. We can use the floor function[14] to calculate the number of integers that are divisible by another integer. For example, and the floor of is 666: . There are 666 numbers among that are divisible by 3. We have

Therefore, the number of that are not multiples of 3, 4, or 5 is

To get the intuition behind the calculation, let’s draw a Venn Diagram. As shown in Figure 3‑18, the circles labeled with 3×, 4×, and 5× represent multiples of 3, 4, and 5, respectively. The intersection of 3× and 4× is labeled 12× as the numbers are multiples of 12. Similarly, we have 15× and 20×. The centerpiece is the intersection of 3×, 4×, and 5×; it is labeled as 60× as the numbers are multiples of 60. Now let’s fill in the numbers for different areas of the Venn Diagram. Typically, we start at the center, There are 33 multiples of 60, so the number at the center is 33. Then we fill the spaces around the center. For example, 166 numbers are multiples of 12. After we exclude multiples of 60, there are 133 numbers in 12× (excluding 60×) area. Similarly, we have 100 in 15× (excluding 60×) and 67 in 20× (excluding 60×). Then, we fill the rest of the areas within the circles. When we add the numbers in these different areas, we get 1200 numbers within the circles. Since there are 2000 numbers in the universal set, 800 numbers are out of the circles.

The Venn Diagram also provides us with the answer to part B. The bottom three areas represent the numbers that are multiples of 3 or 4 but not multiple of 5. Therefore, the total number of possible choices is

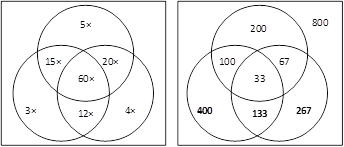
Figure 3‑18 Venn Diagram of integers divisible by 3, 4, or 5.

««« How many rectangles are in Figure 3‑19?

Solution: This problem is a combination of the number of rectangles from a regular shape and inclusion-exclusion rules. We can separate the figure into three areas, a rectangle on the left, a rectangle (the middle two rows), and another rectangle on the right. The total number of rectangles with overcounting is Now we need to remove the double counting. The overlap of the left rectangle with the rectangle is a rectangle. All rectangles in the overlapped rectangle are counted twice. A rectangle has rectangles. Similarly, the overlap of the right rectangle with the rectangle is a rectangle, which also has rectangles counted twice. The total number of overcounting is Therefore, after correcting for overcounting, the total number of rectangles is

Figure 3‑19 Question: Number of rectangles